1(1)
-9x+12x=
そのまま数字(係数)を計算すればいいから、
-9+12=
と同じだよね。
正答率97.4%
1(2)
(-2)×(-3)-4=
掛け算を先に計算するから、まず
(-2)×(-3)=
を計算し、この答えと-4を計算すれば答え。
正答率93.6%
1(3)
60a³b²÷10a²b=
割り算だから、分数にして約分する。
10a²bを分母、60a³b²を分子にして分数にするとどうなるか?
正答率92.9%
1(4)
8÷√2+3√2=
8÷√2は「√2分の8」だが、分数表示ができないので8÷√2とする。
「√2分の8」は分母にルートがあるから、同じ√2を分母と分子にかけて有利化するとどうなるか?
その答えと3√2を計算したものが解答。
正答率70.6%
1(5)
x²-36を因数分解しなさい。
「36」は何の2乗か?
x²-■²=の形はどのように因数分解できるかを覚える。
x²-■²=(x )(x )
正答率87.1%
1(7)
等式6x-3y+21=0を、yについて解きなさい。
「yについて解きなさい」だから「y=」のかたちにする。
正答率67.5%
1(8)
関数y=2x+aのグラフが点(-1、4)を通るとき、aの値を求めなさい。
「点(-1、4)を通る」と言ってるから、(x、y)=(-1、4)を代入すればaの値(切片)が求められる。
正答率79.5%
1(9)
六角柱の辺の本数を答えなさい。
「六角柱」だから底面は「六角」。
底面1面で辺は何本か?
底面は上下あるから・・・。
さらに、側面の縦の辺は何本?
正答率85.3%
1(10)
正十二角形において、∠BACの大きさxを求めなさい。
(正十二角形の1つの内角を頂角とした二等辺三角形の底角の大きさ)
正答率63.5%
1(11)
ある工場には、チョコレートをつくる2種類の機械A、Bが1台ずつあります。
機械Aは150分で4500個のチョコレートをつくり、機械Bは90分で4500個のチョコレートをつくります。
あるとき、チョコレートを、最初は機械Aでつくり、途中から、機械Aを止めて機械Bでつくったところ、つくり始めてから110分で4500個つくることができました。
このとき、次の①、②に答えなさい。
ただし、機械Aも機械Bも、1分間につくるチョコレートの個数はそれぞれ一定とします。
また、機械Aから機械Bに切り替えるのにかかる時間は考えないものとします。
1(11)①
機械Aでチョコレートをつくった時間をx分として、次のような方程式をつくりました。
Zにあてはまる式を、xを使った最も簡単な形で書きなさい。
30x+50(Z)=4500
「最初は機械Aでつくり、途中から、機械Aを止めて機械Bでつくったところ、つくり始めてから110分で」となっているから、
機械Aで作った時間+機械Bで作った時間=110
となる。
「機械Aでつくった時間をx分として」となっているから、これを置き換えると、機械Bで作った時間を表せることができる。
正答率48.4%
1(11)②
機械Aでつくったチョコレートの個数を求めなさい。
上の問題で正しく式が作れれば、それを解いて答えられる問題。
正答率41.7%
2(1)
正答率6.4%→E問題
2(2)
√40+aが整数となるような正の整数aのうち、最も小さい数を求めなさい。
「√40+aが整数となる」ということは「40+a」が何かの数の2乗であれば、√40+aは整数になる。
正答率54.9%
2(3)
正答率24.4%→D問題
2(4)
正答率21%→D問題
2(5)②
正答率8.8%→E問題
3(1)
直線ℓは関数y=xのグラフです。点Aの座標は(16、8)です。点Bはy軸上のy>0の部分にあります。
直線ℓに平行で、点Aを通る直線の式を求めなさい。
「直線ℓに平行」ということから傾きが同じ(xの係数が同じ)。
なので、y=x+bになる。
点A(16、8)を通ると言ってるから、これを代入すればb(切片)が求められる。
正答率42.8%
3(2)
正答率0.3%→E問題
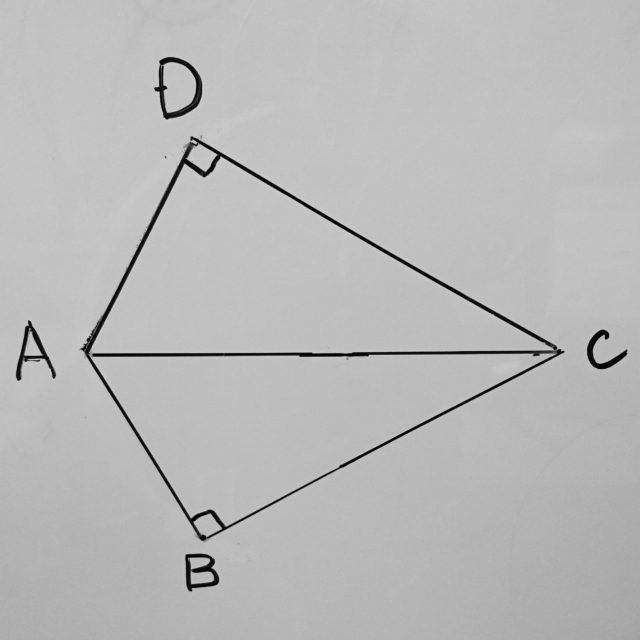
4(1)
∠ABC=∠ADC=90°の四角形ABCDがあります。また、∠BAC=∠DACです。
△ABCと△ADCが合同であることを証明しなさい。
△ABCと△ADCは直角三角形だから、合同条件は
・斜辺と1つの鋭角が等しい
・斜辺と他の1辺が等しい
のどちらかになる。
正答率67.4%
4(2)①
正答率17.3%→E問題
4(2)②
正答率1.2%→E問題